
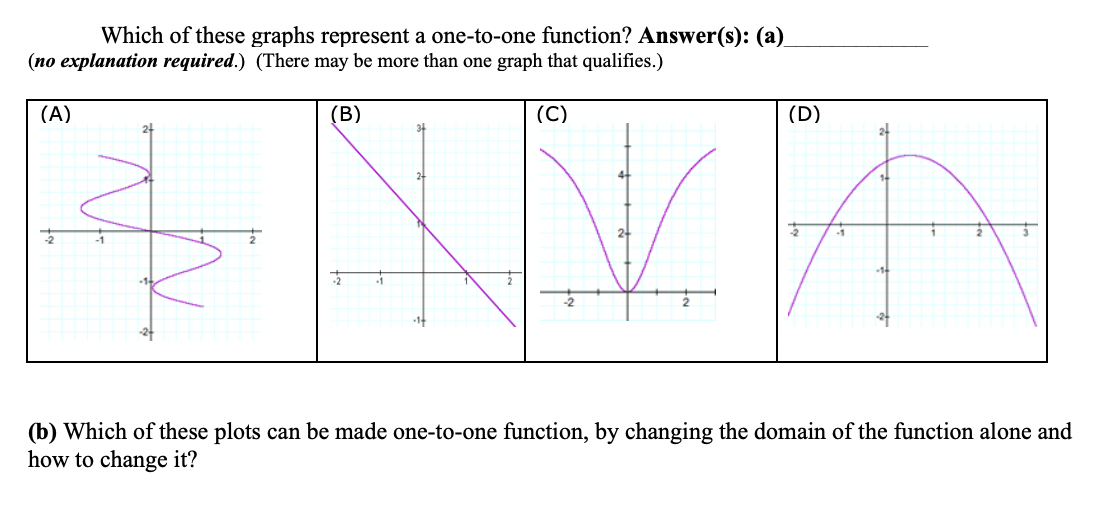
We just proved a one-to-one correspondence between natural numbers and odd numbers. We will use the following “definition”:Ī set is infinite if and only if there is a proper subset and a one-to-one onto (correspondence). A function f from A (the domain) to B (the range) is BOTH one-to-one and onto when no element of B is the image of more than one element in A, AND all elements. There are many ways to talk about infinite sets. So f is one-to-one if no horizontal line crosses the graph more than once, and onto if every horizontal line crosses the graph at least once. He explains an algebraic way to determine if a function is one-to-one. The horizontal line y b crosses the graph of y f(x) at precisely the points where f(x) b.
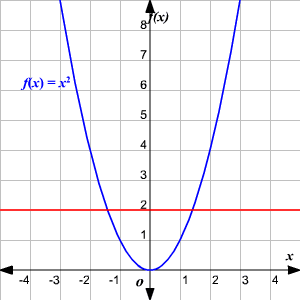
Note that “as many” is in quotes since these sets are infinite sets. He shows two different graphs and performs the line tests to show the best way to do them. There are “as many” prime numbers as there are natural numbers? The graph in figure 3 below is that of a one to one function since for any two different. There are “as many” positive integers as there are integers? (How can a set have the same cardinality as a subset of itself? :-) Explore the definition and properties of one-to-one functions. There are “as many” even numbers as there are odd numbers? We note that is a one-to-one function and is onto.Ĭan we say that ? Yes, in a sense they are both infinite!! So we can say !! Consider a graph of the function (x) sin x or cos x as given in the figure below. Introduction to surjective and injective functionsWatch the next lesson. If b is the unique element of B assigned by the function f to the element a of A, it is written as.
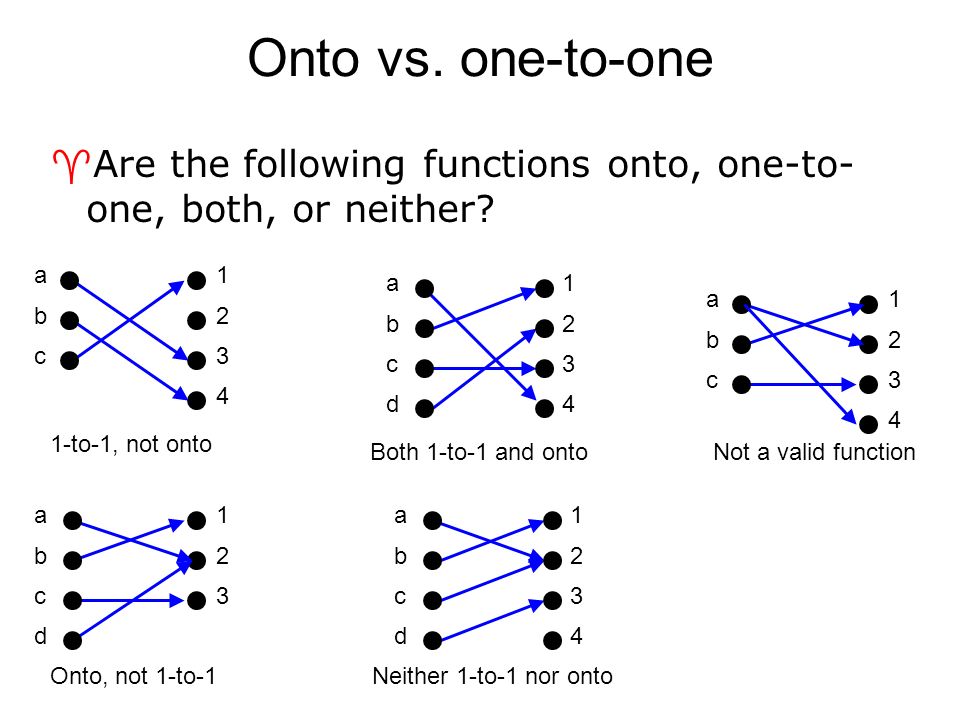
A is called Domain of f and B is called co-domain of f. A function f from A to B is an assignment of exactly one element of B to each element of A (A and B are non-empty sets). If a horizontal line can intersect the graph of the function only a single time, then the function is mapped as one-to-one. Mathematics Classes (Injective, surjective, Bijective) of Functions. There is a one to one correspondence between the set of all natural numbers and the set of all odd numbers. If a horizontal line intersects the graph of the function, more than one time, then the function is not mapped as one-to-one. One-to-One Correspondences of Infinite Set How does the manager accommodate these infinitely many guests? How does the manager accommodate the new guests even if all rooms are full?Įach one of the infinitely many guests invites his/her friend to come and stay, leading to infinitely many more guests. However, the second plot (on the right) is a one-to-one function since it appears to be impossible to draw a horizontal line that crosses the graph more than once. We can detect whether a linear transformation is one-to-one or onto by inspecting the columns of its standard matrix (and row reducing). Let us take, the set of all natural numbers.Ĭonsider a hotel with infinitely many rooms and all rooms are full.Īn important guest arrives at the hotel and needs a place to stay. For the first plot (on the left), the function is not one-to-one since it is possible to draw a horizontal line that crosses the graph twice.
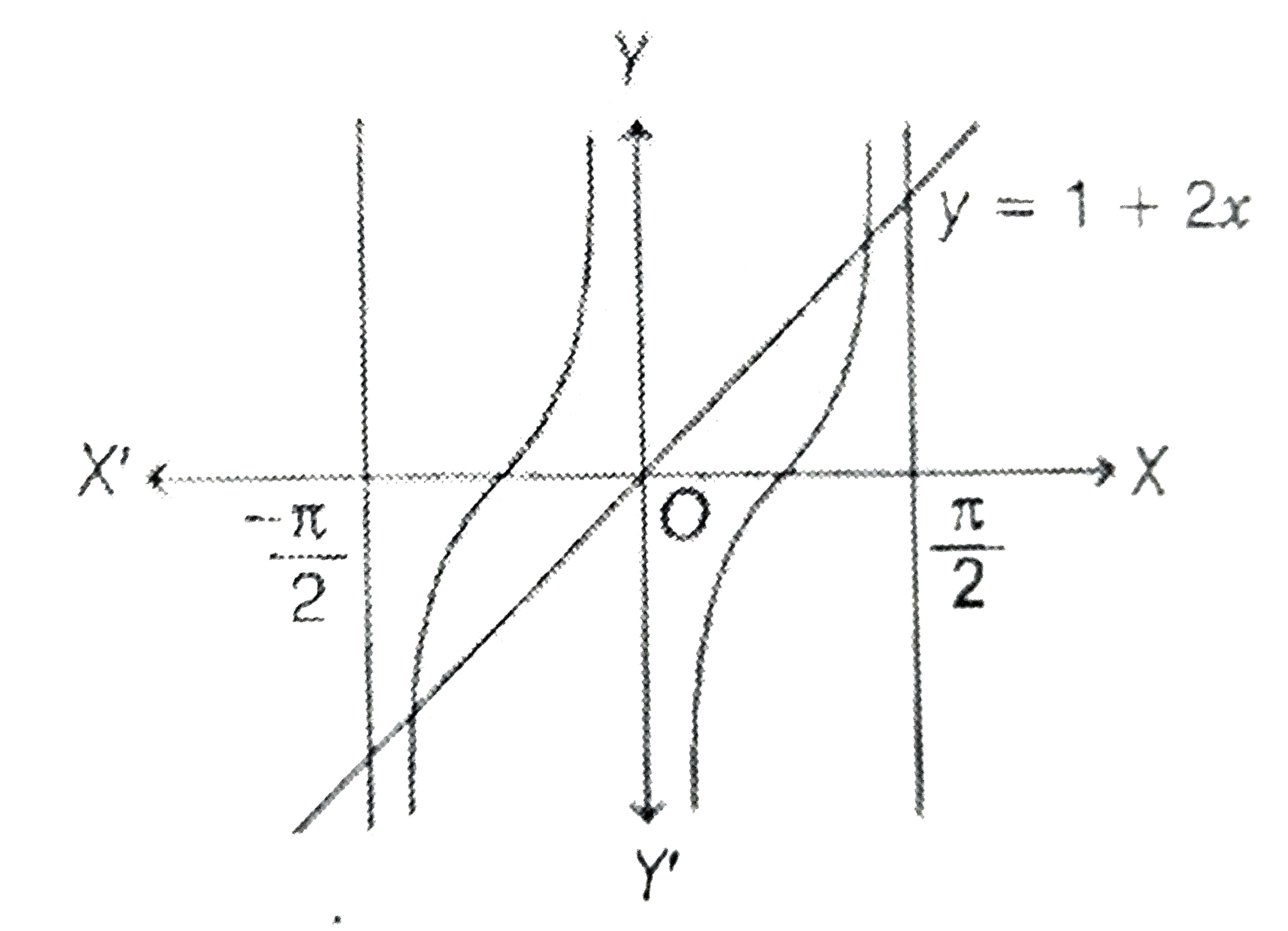
We now note that the claim above breaks down for infinite sets. Illustrate this result on your graph by choosing one value of p. To show a function is a bijection, we simply show that it is both one-to-one and onto using the techniques we developed in the previous sections. Sketch the graph of the function f(x)(x 1)2 + 1 and show that f(p) f(2 p). The last statement directly contradicts our assumption that is one-to-one. A one-to-one correspondence (or bijection) from a set X to a set Y is a function F : X Y which is both one-to-one and onto. Therefore by pigeon-hole principle cannot be one-to-one. Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. Is now a one-to-one and onto function from to. Similarly, we repeat this process to remove all elements from the co-domain that are not mapped to by to obtain a new co-domain. Therefore, can be written as a one-to-one function from (since nothing maps on to ). Let be a one-to-one function as above but not onto.


 0 kommentar(er)
0 kommentar(er)
